經濟管理類本科數學基礎課程教學基本要求
數學與統計學教學指導委員會
一、前言
數學是研究客觀世界數量關系和空間形式的科學.随着現代科學技術和數學科學的發展,“數量關系”和“空間形式”具備了更豐富的内涵和更廣泛的外延.現代數學的内容更豐富,方法更綜合,應用更廣泛.數學不僅是一種工具,而且是一種思維模式;不僅是一種知識,而且是一種素養;不僅是一種科學,而且是一種文化,能否運用數學觀念定量思維是衡量民族科學文化素質的一個重要标志.數學教育在培養高素質經濟和管理人才中越來越顯示出其獨特的、不可替代的重要作用.
高等學校經濟類和管理類專業本科生的數學基礎課程應包括微積分、線性代數與空間解析幾何、概率論與數理統計,它們都是必修的重要基礎理論課.在學習過程中,要将數學知識與其經濟應用有機結合.通過這些課程的學習,應使學生獲得一元函數微積分及其應用、多元函數微積分及其應用、無窮級數、常微分方程與差分方程、向量代數與空間解析幾何、線性代數、概率論與數理統計等方面的基本概念、基本理論、基本方法和運算技能,為今後學習各類後繼課程和進一步擴大數學知識面奠定必要的連續量、離散量和随機量方面的數學基礎.在傳授知識的同時,要注意培養學生進行抽象思維和邏輯推理的理性思維能力,綜合運用所學的知識分析問題和解決問題的能力以及較強的自主學習能力,逐步培養學生的探索精神和創新能力.
課程的教學基本要求,是經濟類和管理類專業本科生學習本課程都應當達到的合格要求,其中帶*号的條目是為某些相關專業選用的,也是對選用專業學生的基本要求.各校各專業根據本校本專業的實際情況,在達到基本要求的基礎上,還可以提出一些較高的或特殊的要求.
各門課程的内容按教學要求的不同,都分為兩個層次.文中用黑體字排印的内容,應使學生深入領會和掌握,并能熟練運用.其中,概念、理論用“理解”一詞表述,方法、運算用“掌握”一詞表述.非黑體字排印的内容,也是必不可少的,隻是在教學要求上低于前者.其中,概念、理論用“了解”一詞表述,方法、運算用“會”或“了解”表述.
基本要求中所列出的各項内容與要求是制訂教學計劃、教學大綱和編寫教材的重要依據,但不涉及課程體系的結構、教學内容的先後安排和編寫教材的章節順序.
二、微積分課程教學基本要求
1. 函數、極限、連續
(1) 在中學已有的基礎上, 加深對函數概念的理解和對函數基本性态(奇偶性、周期性、單調性、有界性)的了解.
(2) 理解複合函數的概念;了解反函數的概念,理解初等函數的概念.
(3) 會建立簡單的經濟問題的函數關系式;了解經濟學中常用的一些函數.
(4) 理解數列極限和函數極限的概念.
(5) 了解無窮大、無窮小、高階無窮小和等價無窮小的概念;會用等價無窮小求極限.
(6) 掌握極限的四則運算法則,會用變量代換求某些簡單複合函數的極限.
(7) 了解極限存在的兩個準則(夾逼準則和單調有界準則);了解兩個重要極限![]() 與
與![]() ,并會用它們求一些相關的極限.
,并會用它們求一些相關的極限.
(8) 理解函數連續的概念;了解函數間斷點的概念, 會判斷間斷點的類型.
(9) 了解初等函數的連續性和閉區間上連續函數的性質(最大值、最小值定理和有界性定理、零點定理和介值定理).
2. 一元函數微分學
(1) 理解導數的概念及其幾何意義和經濟意義(含邊際與彈性的概念),了解函數的可導性與連續性之間的關系.
(2) 掌握基本初等函數的求導公式;掌握導數的四則運算法則和複合函數求導法則;了解反函數的求導法則;掌握隐函數的求導方法.
(3) 了解高階導數的概念,掌握初等函數的一階、二階導數的求法. 了解幾個常見的函數(ex, sin x, cos x, ln(1+x)) 的n階導數的一般表達式.
(4) 理解微分的概念,了解微分概念中包含的局部線性化思想,了解微分的四則運算法則和一階微分的形式不變性.
(5) 理解羅爾(Rolle)定理、拉格朗日(Lagrange)定理及柯西(Cauchy)中值定理,會用洛必達(L’Hospital)法則求不定式的極限.
(6) 了解泰勒(Taylor)定理及用多項式逼近函數的思想(對定理的證明及利用泰勒定理證明相關問題不作要求).
(7) 理解函數的極值概念,掌握利用導數判斷函數的單調性和求極值的方法. 會求解經濟管理問題中的最大值與最小值的應用問題.
(8) 會用導數判斷函數圖形的凹凸性,會求拐點會描繪一些簡單函數的圖形(包括水平和鉛直漸近線).
3. 一元函數積分學
(1) 理解原函數與不定積分的概念;掌握不定積分的性質;了解原函數存在定理.
(2) 掌握不定積分的基本公式;掌握不定積分的換元積分法和分部積分法.
(3) 理解定積分的概念及幾何意義;了解定積分的基本性質和積分中值定理.
(4) 理解變上限的積分作為其上限的函數及其求導定理;掌握牛頓(Newton)—萊布尼茨(Leibniz)公式.
(5) 掌握定積分的換元法與分部積分法.
(6) 掌握實際問題中建立定積分表達式的元素法(微元法),會建立某些簡單的幾何問題及經濟問題的定積分表達式.
(7) 了解兩類反常積分及其收斂性的概念;了解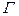 函數的概念.
函數的概念.
4. 無窮級數
(1) 理解無窮級數收斂、發散以及收斂級數和的概念;了解無窮級數的基本性質及收斂的必要條件.
(2) 了解正項級數的比較審斂法,掌握幾何級數與p-級數的斂散性結果;掌握正項級數的比值審斂法.
(3) 了解交錯級數的萊布尼茨定理;了解絕對收斂與條件收斂的概念及二者的關系.
(4) 掌握簡單幂級數收斂區間的求法(區間端點的收斂性不作要求);了解幂級數在其收斂區間内的一些基本性質,會求一些簡單的幂級數的和函數.
(5) 會用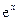 <!--[endif]-->,
<!--[endif]-->,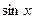 <!--[endif]-->,
<!--[endif]-->,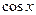 <!--[endif]-->,
<!--[endif]-->,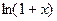 <!--[endif]-->與
<!--[endif]-->與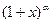 <!--[endif]-->的麥克勞林(Maclaurin)展開式将一些簡單的函數展開成幂級數.
<!--[endif]-->的麥克勞林(Maclaurin)展開式将一些簡單的函數展開成幂級數.
(6) 了解一些無窮級數在經濟中的應用.
5. 向量代數與空間解析幾何
(1) 理解空間直角坐标系的有關概念,會求空間兩點間的距離;理解向量的概念及其表示.
(2) 掌握向量的運算(線性運算、數量積、向量積),了解兩個向量垂直、平等的條件.
(3) 掌握平面的方程和直線的方程及其求法.
(4) 了解曲面方程及空間曲線方程的概念;了解常用二次曲面的方程及其圖形;了解空間曲線的參數方程和一般方程;了解空間曲線在坐标面上的投影.
6. 多元函數微積分學
(1) 理解二元函數的概念及幾何意義;了解多元函數的概念.
(2) 了解二元函數的極限與連續的概念;了解有界閉區域上二元連續函數的性質.
(3) 理解二元函數偏導數與全微分的概念;了解全微分存在的必要條件與充分條件.掌握求偏導數和全微分的方法.
(4) 掌握複合函數一階偏導數的求法,會求複合函數的二階偏導(對抽象複合函數的二階偏導數,隻作簡單訓練).
(5) 會求由一個方程确定的隐函數的一階偏導數.
(6) 理解二元函數極值與條件極值概念;會求二元函數的極值;會用拉格朗日乘數法求條件極值;會求解比較簡單的最大值和最小值問題.
(7) 理解二重積分的概念及幾何意義;了解二重積分性質;掌握二重積分的計算方法(直角坐标,極坐标);會計算無界域上的較簡單的反常二重積分.
*(8) 了解三重積分的概念及計算.
(9) 會用多元函數的微積分知識解決一些簡單的經濟問題.
7. 微分方程與差分方程
(1) 了解微分方程與差分方程的一些基本概念.
(2) 掌握一些基本的一階微分方程(可分離變量方程、齊次方程及一階線性方程)的求解方法.
(3) 掌握一階常系數齊次線性差分方程的求解方法;掌握簡單的一階常系數非齊次線性差分方程的求解方法.
(4) 會用降階法求下列三種類型的高階方程: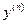 <!--[endif]-->= f (x),
<!--[endif]-->= f (x), 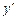 <!--[endif]-->=f (x, y),
<!--[endif]-->=f (x, y), 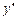 <!--[endif]-->= f (y,
<!--[endif]-->= f (y, 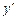 <!--[endif]-->).
<!--[endif]-->).
(5) 了解二階線性微分方程和差分方程解的結構;會求解二階常系數的齊次線性微分方程和差分方程;會求解一些簡單的二階常系數的非齊次線性微分方程和差分方程.
(6) 會通過建立微分方程和差分方程模型,解決一些簡單的經濟問題.
三、線性代數課程教學基本要求
1. 行列式
(1) 了解行列式的概念, 掌握行列式的基本性質.
(2) 會應用行列式的定義、性質和有關定理計算行列式.
(3) 了解克拉默法則.
2. n維向量
(1) 理解n維向量的概念,理解向量的線性組合和線性表示的概念.掌握向量的加法和數乘運算.
(2) 理解向量組的線性相關和線性無關的定義;會判斷向量組的線性相關性或線性無關性.
(3) 理解向量組的極大線性無關組和向量組的秩的概念;會求向量組的極大線性無關組和秩.
3. 矩 陣
(1) 理解矩陣的概念.
(2) 了解單位矩陣、對角矩陣、三角矩陣、對稱矩陣、反對稱矩陣以及它們的性質.
(3) 掌握矩陣的加法、數乘、乘法、轉置以及它們的運算規律;了解方陣的幂、方陣乘積的行列式的性質.
(4) 理解逆矩陣的概念;掌握矩陣可逆的充分必要條件;了解伴随矩陣與逆矩陣的關系;掌握逆矩陣的性質.
(5) 掌握矩陣的初等變換;了解初等矩陣的性質和矩陣等價的概念.
(6) 了解矩陣秩的概念;了解向量組的秩與矩陣的秩之間的關系.
(7) 掌握用初等變換求矩陣的秩和求逆矩陣的方法.
4. 線性方程組
(1) 理解齊次線性方程組有非零解的充分必要條件及非齊次線性方程組有解的充分必要條件.
(2) 理解齊次線性方程組的基礎解系和通解的概念.
(3) 理解非齊次線性方程組解的結構及通解的概念.
(4) 掌握用初等變換求線性方程組通解的方法.
5. 向量空間
(1) 了解n維向量空間、線性子空間、基底、維數、坐标等概念;了解向量在不同基底下的坐标變換.
(2) 了解向量内積的定義;掌握線性無關向量組的正交化方法.
(3) 了解正交矩陣的定義及主要性質.
6. 矩陣的特征值與特征向量
(1) 了解矩陣特征值、特征向量等概念及有關性質.會求矩陣特征值和特征向量.
(2) 了解相似矩陣的概念.
(3) 掌握将實對稱矩陣化為對角陣的方法.
*(4) 了解向量和矩陣序列極限的概念;了解矩陣級數的收斂性及收斂條件.
*(5) 了解投入産出數學模型.
7. 二次型
(1) 了解二次型的概念;會用矩陣形式表示二次型.
(2) 了解合同變換和合同矩陣的概念;了解二次型的秩的概念;了解二次型的标準形、規範形等概念;了解慣性定理的條件和結論;會用正交變換和配方法化二次型為标準形.
(3) 理解正定(負定)二次型、正定(負定)矩陣的概念;掌握正定矩陣的基本性質;了解二次型在求極值問題中的應用.
四、概率論與數理統計課程教學基本要求
1. 随機事件與概率
(1) 了解随機現象與随機試驗,了解樣本空間的概念,理解随機事件的概念,掌握事件之間的關系與運算.
(2)了解事件頻率的概念、了解概率的統計定義.了解概率的古典定義,會計算簡單的古典概率.
(3) 了解概率的公理化定義,理解概率的基本性質,理解概率加法定理.
(4) 了解條件概率的概念. 理解概率的乘法定理. 了解全概率公式,理解貝葉斯(Bayes)公式,并會應用貝葉斯公式解決較簡單問題.
(5) 理解事件的獨立性概念. 了解伯努利(Bernoulli)概型和二項概率的計算方法.
2. 随機變量及其分布
(1) 理解随機變量的概念,了解分布函數的概念和性質,會計算與随機變量相聯系的事件的概率.
(2) 理解離散型随機變量及其分布律的概念,掌握0-1分布、二項分布和泊松(Poisson)分布.
(3) 理解連續型随機變量及其概率密度的概念,掌握正态分布、均勻分布和指數分布.
(4) 會根據自變量的概率分布求其簡單随機變量函數的概率分布.
3. 多維随機變量及其分布
(1) 了解多維随機變量的概念,理解二維随機變量的分布函數的概念.
(2) 理解二維離散型随機變量的分布律的概念,理解二維連續型随機變量的概率密度的概念.
(3) 理解二維離散型随機變量的邊緣分布律,理解二維連續型随機變量的邊緣概率密度.
(4) 理解随機變量的獨立性概念.
(5) 會求兩個獨立随機變量簡單函數的分布(和、極大、極小),了解有限個正态分布的線性組合仍是正态分布的概念.
4. 随機變量的數字特征
(1) 理解随機變量數學期望與方差的概念,掌握它們的性質與計算.會求随機變量函數的數學期望.
(2) 掌握0-1分布、二項分布、泊松分布、正态分布、均勻分布和指數分布的數學期望與方差.
(3) 了解矩、協方差、相關系數的概念及其性質,并會計算.
(4) 了解随機變量的數字特征在經濟中的應用.
5. 大數定律和中心極限定理
(1) 了解切比雪夫(Чебйыев)不等式,切比雪夫大數定律和伯努利大數定律,了解伯努利大數定律與概率的統計定義、參數估計之間的關系.
(2) 了解棣莫弗-拉普拉斯(De Moivre-Laplace)中心極限定理,并會運用該定理近似計算有關事件的概率.
(3) 了解獨立同分布的中心極限定理.
6. 數理統計的基本概念
(1) 理解總體、個體、樣本和統計量的概念.
(2) 了解直方圖的作法.
(3) 理解樣本均值、樣本方差的概念,掌握根據數據計算樣本均值、樣本方差的方法.
(4) 了解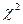 <!--[endif]-->分布,
<!--[endif]-->分布,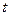 <!--[endif]-->分布,
<!--[endif]-->分布,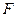 <!--[endif]-->分布的定義,并會查表計算分位數.
<!--[endif]-->分布的定義,并會查表計算分位數.
(5) 了解正态總體的常用抽樣分布.
(6) 了解經驗分布函數的概念和性質,會根據樣本值求經驗分布函數.
7. 參數估計
(1) 理解點估計的概念,掌握矩估計法與極大似然估計法.
(2) 了解估計量的評判标準(無偏性、有效性、一緻性).
(3) 理解區間估計的概念,會求單個正态總體均值與方差的置信區間,會求兩個正态總體均值差與方差比的置信區間.
8. 假設檢驗
(1) 理解假設檢驗的基本思想,掌握假設檢驗的基本步驟,了解假設檢驗可能産生的兩類錯誤.
(2) 了解單個正态總體均值與方差的假設檢驗,了解兩個正态總體均值差與方差比的假設檢驗.
*(3) 了解總體分布假設的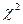 <!--[endif]-->檢驗法,會應用該方法進行分布拟合優度檢驗.
<!--[endif]-->檢驗法,會應用該方法進行分布拟合優度檢驗.
9. 回歸分析
*(1) 了解回歸分析的含義.
*(2) 會用最小二乘法求回歸系數;了解可線性化為一元線性回歸的基本類型.
*(3) 會作簡單預測.
五、建 議
(1) 随着社會的發展,經濟管理領域對數學的要求越來越高,經濟管理類專業數學具有越來越強烈的應用背景.學校和教師在經濟管理類數學課程的教學中應努力聯系本專業的實際,以提高學生學習數學的興趣和應用數學知識解決本專業實際問題的意識和能力.要努力收集數學在經濟管理中鮮活的應用案例,引入教學和教材.在引入數學知識時也應提倡從解決經濟管理領域中的适當的實際問題入手,通過建立數學模型解決這些實際問題的過程來引入數學的概念、思想和方法.在教學實踐中不斷改革創新,逐步形成适應現代社會發展中經濟管理實際的數學教學内容體系.
(2) 各校應根據自身的實際情況,努力創造條件,以适當的形式開設與理論教學相配套的數學建模和數學實驗課,或在現有數學課程教學中适當安排數學建模和數學實驗的内容,培養學生建立數學模型并借助于數學軟件解決經濟和管理問題的能力.
(3) 積極進行教學方法與教學手段的改革,不斷探索以學生為主體有利于調動學生自主學習積極性的啟發式、讨論式、研究式的教學方法.要積極采用現代教育技術手段,使傳統的教學手段與現代教學手段相互結合,取長補短.
(4) 為達到本課程教學基本要求,需要有相應的教學課時.建議微積分、線性代數、概率論與數理統計各部分的學時分别不低于144、36和54.
(5) 希望各校在教學過程中不斷總結經驗,就如何改進和加強經濟類數學課程的教學提出意見和建議.
